Graphes I

Table des matières

1. Les graphes
- 1.1. Définitions
- 1.2. Modélisation
2. Représentations d'un graphe
3. Parcours en profondeur d'un graphe
4. Compléments
- 4.1. Parcours eulérien et hamiltonien
- 4.2. Graphes planaires
  - Graphe dual
  - Triangulation

1. Les graphes

1.1. Définitions

Un graphe orienté (simple) $\mc G$ est la donnée $\mc G = (S, A)$ d'un ensemble $S$ de sommets, et d'un ensemble $A \subset S^2$ d'arcs, avec la convention que $(i,j)\in A$ s'il y a un arc reliant le sommet $i$ au sommet $j$. On notera $i\ra j$ si $(i,j)\in A$.
Un graphe non orienté est un graphe dans lequel les arcs (appelés arêtes) n'ont pas d'orientation. On peut le représenter comme précédemment $\mc G = (S, A)$, avec la propriété $(i,j)\in A\ssi (j,i)\in A$.
Une boucle est un arc qui va d'un sommet à lui-même. On conviendra que les graphes non orientés n'ont jamais de boucles.

Pour un graphe orienté $\mc G$ à $n$ sommets. Quel est le nombre maximal d'arcs possibles ? et si $\mc G$ n'a pas de boucle ?
Pour un graphe non orienté $\mc G$ à $n$ sommets sans boucle. Quel est le nombre maximal d'arêtes possibles ?
★ Quel est le nombre de graphes orientés à $n$ sommets ? Non orientés ?

Soit $n\in\N^*$, on appelle

graphe complet à $n$ sommets, noté $K_n$, le graphe non orienté à $n$ sommets sans boucle dont toutes les paires de sommets distincts sont reliées par une arête.
graphe nul à $n$ sommets, noté $N_n$, le graphe non orienté à $n$ sommets sans arête.

Soit $\mc G = (S, A)$ un graphe et $s\in S$ un sommet

Si $\mc G$ est non orienté, on appelle voisinage de $s$, l'ensemble des sommets $s'$ reliés à $s$ par une arête.
Si $\mc G$ est orienté, on appelle
- successeur de $s$ tout sommet $s'$ tel que $s\ra s'$.
- prédécesseur de $s$ tout sommet $s'$ tel que $s'\ra s$.

Soit $\mc G = (S, A)$ un graphe et $s\in S$ un sommet

Si $\mc G$ est non orienté,
- on appelle degré de $s$, noté $d(s)$, le nombre de voisins de $s$.
- on dit que $\mc G$ est régulier si tous ses sommets ont le même degré.
Si $\mc G$ est orienté, on appelle
- degré sortant de $s$, noté $d_+(s)$, le nombre de successeurs de $s$.
- degré entrant de $s$, ($d_-(s)$), le nombre de prédécesseurs de $s$.

Si $\mc G$ est un graphe, dont $V$ est l'ensemble des sommets, et $m$ est le nombre d'arcs/d'arêtes.

Si $\mc G$ est orienté, on a $$\sum_{s\in V} d_+(s) = \sum_{s\in V} d_-(s) = m.$$
Si $\mc G$ est non orienté, on a $$\sum_{s\in V} d(s) = 2m.$$

Soit $\mc G$ un graphe non orienté. Montrer que le nombre de sommets de degré impair est pair.

1.2. Modélisation

Quelques situations et problèmes qui peuvent se modéliser par des graphes.

Réseau routier

Un réseau de transport est naturellement représenté par un graphe, dont les sommets sont les intersections (ou les villes, à plus grande échelle), et les arêtes ou arcs sont les routes.

On peut étiqueter les arêtes d'information supplémentaire comme

la longueur de la route
son prix (péage, ou vol d'avion, etc)

puis rechercher un chemin d'un sommet à un autre de longueur/prix minimal.

Internet

Google s'est originellement rendu célèbre par son algorithme PageRank de tri des résultats des recherches. Celui-ci utilise un graphe, dont les sommets sont les pages webs, et les arcs sont les liens d'une page à une autre, pour attribuer à chaque page une importance.

Le web recense actuellement $\simeq 5$ milliards de pages web.

Réseau social

Tout réseau social avec un système de «Follow» peut être représenté par un graphe orienté, dont les sommets sont les utilisateurs, et $A\ra B$ signifie que $A$ «follows» $B$.

Le degré entrant d'un sommet représente la popularité de l'utilisateur. La topologie du graphe peut révéler des groupements d'utilisateurs, et des bulles d'opinion.

Positions d'un jeu

On peut modéliser un jeu comme les échecs par un graphe, dont les sommets sont les états possibles de l'échiquier, et deux sommets sont reliés par un arc si on peut passer de l'un à l'autre par un coup légal. Il y a un sommet initial, correspondant à la position initiale de l'échiquier, et des sommets finaux, correspondant aux positions d'échec et mat.

Au jeu d'échec, le nombre de position légales est de l'ordre de $10^{40}$.

2. Représentations d'un graphe

Il existe plusieurs façons de représenter un graphe en informatique.

2.1. Représentation par la matrice d'adjacence

Soit $\mc G = (S, A)$ un graphe dont l'ensemble des sommets est $S = \db{1,n} = \{1, \dots, n\}$. On appelle matrice d'adjacence de $\mc G$ la matrice $M = \left(m_{ij}\right)_{i,j\leq n}\in\M_n(\R)$, où $m_{ij} = \begin{cases} 1 \si (i,j)\in A\\ 0 \sinon \end{cases}$.

Déterminer la matrice d'adjacence du graphe de droite.
Quelle est la matrice d'adjacence du graphe complet $K_n$ ?
Que dire de la matrice d'adjacence d'un graphe non orienté ?

En Python, on choisit plutôt $\db{0,n-1}$ comme ensemble de sommets.

On représente la matrice d'adjacence par une liste M de listes d'entiers. Pour $i,j\in\db{0,n-1}$, M[i][j] vaudra $1$ s'il existe un arc $i\ra j$, et $0$ sinon.
On peut utiliser la syntaxe suivante
```
[[0] * n for _ in range(n)]
```
Un test de la forme if M[i][j] == 1: peut s'écrire simplement if M[i][j]:, Python convertissant automatiquement les entiers $1$ et $0$ en booléens True et False.

Écrire une fonction matrice_graphe_complet qui prend en argument un entier $n\geq 1$ et renvoie la représentation par matrice d'adjacence du graphe complet $K_n$ sur l'ensemble des sommets $\db{0,n-1}$.

Écrire une fonction successeurs qui prend en argument un graphe représenté par sa matrice d'adjacence, et un sommet $s$ et renvoie la liste des successeurs de $s$.

2.2. Représentation par listes d'adjacences

On peut représenter un graphe $\mc G$ dont l'ensemble des sommets est $\db{0,n-1}$ par une liste de listes L telle que, pour tout $i\in\db{0,n-1}$, L[i] contienne la liste des successeurs du sommet i.

Donner la représentation par listes d'adjacence du graphe ci-contre.

Écrire une fonction listes_graphe_complet qui prend en argument un entier $n\geq 1$ et renvoie la représentation par listes d'adjacence du graphe complet $K_n$ sur l'ensemble des sommets $\db{0,n-1}$.

Écrire une fonction matrice_adj qui prend en argument une liste L représentant un graphe $\mc G$ par listes d'adjacence et qui renvoie la matrice d'adjacence du graphe $\mc G$.
On suppose que le graphe $\mc G$ a $n$ sommets.
1. Quelle est, en fonction de $n$, la complexité de votre implémentation dans le pire des cas ?
2. Si ce n'est pas déjà le cas, proposer une implémentation en $O(n^2)$.

Variantes de la représentation par listes d'adjacence

On peut utiliser un dictionnaire D pour stocker les listes d'adjacences. Cela permet d'utiliser un autre ensemble que $\db{0,n-1}$ pour les sommets. Par exemple, on peut prendre $V = \{A, B, C\}$ et accéder à la liste des successeurs de $A$ par D["A"].
Au lieu d'une liste d'adjacence L[s] = [s1, s2, ..., sk] contenant les voisins d'un sommet $s$, on peut utiliser un dictionnaire d'adjacence, représentant l'ensemble des voisins, comme d = {s1: None, s2: None, ..., sk: None}.

L'avantage est de pouvoir tester si $j$ est un successeur de $i$ en temps constant, via j in L[i].

2.3. Performance des différentes représentations

Si $\mc G$ est un graphe à $n$ sommets et $m$ arcs,

Coût mémoire de la représentation

la matrice d'adjacence a un coût mémoire en $O(n^2)$
la liste de listes d'adjacence a un coût mémoire en $O(n + m)$

Appartenance d'un arc

Tester si un arc $(i,j)$ appartient au graphe ou non a une complexité

en $O(1)$ pour la matrice d'adjacence : il suffit de regarder M[i][j].
en $O(n)$ dans le pire des cas pour la représentation en listes d'adjacence : il faut tester si $j\in \texttt{L[i]}$

Degré (sortant) d'un sommet

Déterminer le degré d'un sommet $i$ a une complexité

en $O(n)$ pour la matrice d'adjacence : il faut compter le nombre de $1$ dans la liste M[i]
en $O(1)$ pour la représentation en listes d'adjacence : le degré de $i$ s'obtient avec len(L[i]).

2.4. Exercices

Écrire une fonction taille qui prend en argument un graphe $\mc G$ et qui renvoie un couple $(n,m)$, où $n$ est le nombre de sommets de $\mc G$, et $m$ est le nombre d'arcs de $\mc G$.

si le graphe $\mc G$ est donné par sa matrice d'adjacence.
si le graphe $\mc G$ est donné par ses listes d'adjacence.

Écrire une fonction predecesseurs qui prend en argument un graphe $\mc G$ et un sommet $s$ de $\mc G$ et qui renvoie la liste des prédécesseurs de $s$.

si le graphe $\mc G$ est donné par sa matrice d'adjacence.
si le graphe $\mc G$ est donné par ses listes d'adjacence.

Écrire une fonction regulier qui prend en argument un graphe $\mc G$ non orienté donné par ses listes d'adjacence et renvoie True si le graphe $\mc G$ est régulier, et False sinon.

Écrire une fonction deg_max qui prend en argument un graphe $\mc G$ non orienté donné par sa matrice d'adjacence et renvoie le degré maximal des sommets de $\mc G$.

Écrire une fonction non_oriente qui prend en argument un graphe $\mc G$ donné par sa matrice d'adjacence et renvoie True si on peut considérer que le graphe $\mc G$ est non orienté et sans boucle, et False sinon.

Écrire une fonction successeurs_communs qui prend en argument un graphe $\mc G$ et deux sommets s1 et s2 et qui renvoie une liste des successeurs communs à s1 et s2.
1. Si le graphe $\mc G$ est donné par ses listes d'adjacence.
2. Si le graphe $\mc G$ est donné par sa matrice d'adjacence.
Quelle est, pour chaque représentation et dans le pire des cas, la complexité de votre fonction, en fonction du nombre $n$ de sommets de $\mc G$ ?
Proposer une solution d'une complexité en $O(n)$ dans le cas d'une représentation par les listes d'adjacences.

Le graphe inverse d'un graphe orienté est le graphe obtenu en inversant le sens de toutes les arcs de $\mc G$. Écrire une fonction transpose qui prend en argument un graphe et renvoie le graphe inverse.

Si $\mc G$ est représenté par sa matrice d'adjacence.
Si $\mc G$ est représenté par ses listes d'adjacence.
Quelle est la complexité, dans chaque cas, en fonction du nombre de sommets $n$ et du nombre d'arcs $m$ du graphe ?

Essayez : transpose_mattranspose_listesQuestion Complexité

2.4.1. Chemins

On appelle chemin dans un graphe $\mc G = (S, A)$ toute suite de sommets $s_1, s_2, \dots, s_n$ telle que pour tout $i\in\db{1,n-1}$, $s_i \ra s_{i+1}$. On note alors $s_1 \ra s_2 \ra \dots \ra s_n$ ce chemin, qui relie $s_1$ à $s_n$. Il est dit fermé si $s_1 = s_n$.

Écrire une fonction est_chemin qui prend en argument un graphe $G$ (que l'on représentera au choix), et une liste l de sommets, et qui renvoie True ssi cette liste représente un chemin.

Soit $G$ un graphe orienté, pour lequel $\forall s\in S,\,d_+(s)\gt 0$.

Justifier que $G$ admet un cycle, c'est-à-dire un chemin fermé non trivial (de longueur $\geq 1$).
Écrire une fonction extraire_cycle qui prend en argument un tel graphe, et renvoie un tel chemin.

On veut une complexité en $O(n)$, où $n = |S|$.

2.4.2. Puissances de la matrice d'adjacence

Si $A$ est la matrice d'adjacence d'un graphe, pour tout $n\geq 0$, $(A^n)_{ij}$ est le nombre de chemins de longueur $n$ reliant $i$ à $j$.

Démontrer le théorème précédent.

Implémenter une fonction produit_mat qui multiplie deux matrices carrées de même taille. Complexité ?

Il existe des algorithmes plus efficaces (comme celui de Strassen), avec des complexités en $O(n^{\b})$, pour $2\lt \b\lt 3$. La complexité optimale est un problème ouvert.

${}$

On représente un graphe orienté sans boucles par sa matrice d'adjacence.

On cherche si le graphe contient un $3$-cycle, c'est-à-dire un triplet de sommets $s_1,s_2,s_3$ tels que $s_1 \ra s_2 \ra s_3 \ra s_1$.
1. Proposer une fonction a_triangle naïve. Complexité ?
2. Proposer une fonction a_triangle_bis qui utilise les matrices $A^2$ et $A$. Complexité ?
Écrire une fonction appartient_quatre_cycle qui prend en argument un sommet $s$ du graphe et décide si ce sommet appartient à un $4$-cycle, avec une complexité en $O(n^2)$.

Soit $A\in\M_n(\R)$ une matrice à coefficients positifs, vérifiant $\forall i,\, a_{ii}\gt 0$. Montrer qu'il existe un entier $N$ tel que $$\forall i,j\in\db{1,n},\,\forall k\geq N,\quad A^k_{ij}\gt 0 \ssi A^N_{ij}\gt 0.$$
On note $N$ le plus petit tel entier. Justifier que $N\leq n-1$.
Soit $B$ la matrice d'adjacence d'un graphe $\mc G$ orienté sans boucles, et $A = I_n + B$. Interpréter les coefficients de $A^k$, en termes de $\mc G$. À quoi correspond l'entier $N$ ?
En utilisant les fonctions précédentes, écrire une fonction joignable qui prend en argument le graphe, et deux sommets $i,j$ et renvoie True ssi il existe un chemin reliant $i$ à $j$.

Quelle est la complexité de cette implémentation ?

2.4.3. Graphes bipartis

Un graphe $\mc G$ est dit biparti s'il existe une partition $S = S_1 \sqcup S_2$ de ses sommets telle que $A \subset S_1\times S_2 \cup S_2 \times S_1$. Autrement dit, telle que les arcs de $\mc G$ ne relient que des sommets de $S_1$ à $S_2$, ou des sommets de $S_2$ à $S_1$.

Le graphe biparti complet $B_{n,m}$ est le graphe non orienté, sur $S = \db{1,n+m}$ dont les arêtes sont exactement celles reliant les sommets de $\db{1,n}$ aux sommets de $\db{n+1,n+m}$. Écrire une fonction biparti_complet qui prend en argument $n,m$ et renvoie la matrice d'adjacence de $B_{n,m}$.
Écrire une fonction est_biparti qui prend en argument un graphe $\mc G$, d'ensemble des sommets $\db{0,n-1}$, sous la forme de ses listes d'adjacence, ainsi qu'une partition p, représentée par une liste de taille $n$ à valeurs dans $\{0,1\}$ et vérifie si le graphe $\mc G$ est bien biparti, pour cette partition.

Essayez : biparti_completest_biparti

On note $N$ le diamètre du graphe, et $M$ le plus petit indice, s'il existe, tel que $\forall i,j,\, (A^M)_{ij}\gt 0$. Sinon, on pose $M = +\i$.

Justifier que $M\geq N$.
Soit $G$ biparti. Montrer que $M = +\i$.
★ Soit $C_i, C_j$ deux colonnes distinctes de $A^N$. Montrer que si elles sont orthogonales, alors $G$ est biparti.
★ Soit $G$ non biparti, montrer que $M\leq 2N$.
En déduire une fonction est_biparti qui décide si un graphe est biparti.

3. Parcours en profondeur d'un graphe

Dans cette partie, sauf mention du contraire, les graphes sont représentés par leurs listes d'adjacence.

3.1. Premier exemple : atteignabilité

S'il existe un chemin d'un sommet $s_1$ à un sommet $s_2$, on dit que $s_2$ est atteignable depuis $s_1$. Par convention, $s_1$ est toujours atteignable depuis $s_1$ (par le chemin vide).

Étant donné un graphe $\mc G$, (représenté par ses listes d'adjacence), et un sommet $d$, on veut déterminer la liste des sommets atteignables depuis $d$.

Compléter la fonction atteignables ci-dessous, prenant en argument $\mc G$ et d, et qui renvoie la liste des sommets de $\mc G$ atteignables depuis le sommet d.

Elle utilise une liste de sommets a_traiter comme une pile : on y ajoute, puis retire des sommets, avec append et pop.

    def atteignables(g, d):
        vus = [d]
        a_traiter = [d]
        while a_traiter != []:
            s = a_traiter.pop()
            …
            …
        return vus

Amender la fonction précédente pour remplacer la liste vus par un dictionnaire vus, dont les clefs sont les sommets vus, et les valeurs sont des None. Quel est l'intérêt ?
Pour le graphe $\mc G$ donné plus bas, décrire l'ordre dans lequel les sommets de $\mc G$ sont traités, pour un parcours partant du sommet $A$. On supposera que les listes d'adjacences sont triées par ordre alphabétique. Ce parcours est dit en profondeur.

\hfill

Si le graphe $\mc G$ a $n$ sommets et $m$ arcs, la complexité du parcours en profondeur précédent utilisant un dictionnaire est en $O(m)$.

Chaque itération de la boucle principale traite un sommet, et chaque sommet n'est traité au plus qu'une fois, la boucle principale tourne donc au plus une fois sur chaque sommet. De plus, pour chaque tel sommet $s$, la boucle intérieure s'exécute une fois pour chaque successeur de $s$.

On en déduit que la boucle intérieure s'exécutera au plus une fois pour chaque arc du graphe, et comme l'intérieur de la boucle a une complexité constante, la complexité totale est en $O(m)$.

En utilisant une liste au lieu d'un dictionnaire pour vus, elle contient au plus $n$ éléments, dont les appels a in vus ont une complexité en $O(n)$, et la complexité totale est en $O(nm)$.
Le parcours donné ne parcourt pas nécessairement tout le graphe, uniquement les «descendants» du sommet initial.

La fonction récursive suivante prend en argument un graphe L, représenté par ses listes d'adjacence, un sommet s et une liste vus de sommets à éviter, et réalise un parcours en profondeur (en imprimant les sommets) par des appels récursifs.

En utilisant la fonction auxiliaire parcours_prof_aux, écrire une fonction parcours_profondeur qui prend en argument un graphe et un sommet initial et réalise un parcours en profondeur partant de ce sommet.
Sur le graphe donné, décrire l'ordre de ce parcours en profondeur. Comment le qualifier par rapport au parcours en profondeur précédent ?

def parcours_prof_aux(L, s, vus):
    for v in L[s]:
        if v not in vus:
            print(v)
            vus.append(v)
            parcours_prof_aux(L, v, vus)

\hfill

3.2. Connexité

Un graphe non orienté $\mc G$ est dit connexe si toute paire de sommets distincts sont reliés par un chemin.
La composante connexe d'un sommet $s\in G$ est l'ensemble des sommets atteignables depuis $s$.
Un graphe orienté est dit fortement connexe, si pour toute paire $(s_1,s_2)$ de sommets distincts, il existe un chemin de $s_1$ à $s_2$, et un chemin de $s_2$ à $s_1$.

Les composantes connexes d'un graphe non orienté sont les classes d'équivalences pour la relation $x\sim y$ s'il existe un chemin de $x$ à $y$. Elles forment une partition de l'ensemble des sommets du graphe.

Soit $\mc G$ un graphe non orienté, et $s_0$ un sommet de $\mc G$. Alors $\mc G$ est connexe si et seulement si pour tout sommet $s$ différent de $s_0$, il existe un chemin de $s_0$ à $s$.

En utilisant la fonction atteignables précédente, écrire une fonction est_connexe qui prend en argument un graphe $\mc G$ non orienté et renvoie True si le graphe $\mc G$ est connexe.

3.3. Chemins

Écrire une fonction existe_chemin qui prend en argument un graphe $\mc G$, un sommet $d$ et un sommet $f$ et qui renvoie True s'il existe un chemin de $d$ à $f$. Complexité ?

On s'inspirera de la fonction atteignables (mais on ne l'utilisera pas).

Écrire une fonction récursive existe_chemin_aux qui prend en argument un graphe $\mc G$, une liste l de sommets à éviter, un sommet d et un sommet f et qui renvoie True s'il existe un chemin de d à f, sans passer par les sommets de l.
En utilisant la fonction auxiliaire précédente, écrire une fonction existe_chemin_bis.

On peut a priori identifier un parcours en profondeur à l'ordre dans lequel il visite les sommets du graphes.

En fait un parcours de graphe correspond plutôt à une liste ordonnée des arcs que l'on emprunte, chacun allant d'un sommet déjà visité à un nouveau sommet.

Un parcours d'un graphe définit alors une relation de parenté : Mis à part le sommet initial, à chaque autre sommet $s$ visité, on peut associer un unique parent $s'$ dans le parcours : c'est l'origine de l'unique arc $s'\ra s$ du parcours pointant sur $s$.

On suppose donnée une liste parent de taille $n$, qui à chaque sommet associe son parent dans un parcours en profondeur issu d'un sommet $d$, ou None s'il n'en a pas.

Écrire une fonction reconstitue_chemin, qui prend en argument la liste parent, le sommet $d$, et un sommet final $f$, et renvoie un chemin de $d$ à $f$, ou None s'il n'en existe pas.
En déduire une fonction chemin qui prend en argument un graphe, et deux sommets, et qui renvoie un chemin entre les deux sommets donnés, sous la forme d'une liste de sommets, ou None, s'il n'existe pas de tel chemin.

Écrire une version récursive qui prend en argument $\mc G$ et deux sommets $i,j$ et renvoie un chemin de $i$ à $j$, ou None s'il n'en existe pas.

3.4. ★ «Vrai» parcours en profondeur

On cherche à parcourir un graphe $\mc G$ «en profondeur», en affichant les sommets, dans l'ordre dans lequel ils sont traités.

Si $v$ est un sommet de $\mc G$, on note $\mc D_{v}$ l'ensemble des descendants de $v$ (c'est-à-dire les sommets $w$ tels que il existe un chemin de $v$ à $w$).
Si $\mc P$ est un «parcours» de $\mc G$, que l'on identifie avec l'ordre dans lequel les sommets sont traités, on note $\mc D^{\mc P}_{v, +}$ l'ensemble des descendants de $v$ qui sont traités après $v$.
Si $w\in \mc D_v$, on note $v \twoheadrightarrow_{\mc P} w$ si $w$ est traité après $v$ et que tous les sommets traités entre $v$ et $w$ sont des descendants de $v$.

Un parcours $\mc P$ est dit en profondeur (pour de vrai…) si $\forall v\in S,\, \forall w\in \mc D^{\mc P}_{v,+},\, v\twoheadrightarrow_{\mc P} w$.

Justifier par un exemple que le parcours «en profondeur» implémenté itérativement précédemment n'est pas un vrai parcours en profondeur.
★ Démontrer que le parcours en profondeur récursif implémenté précédemment est un vrai parcours en profondeur.
Proposer une implémentation itérative d'un vrai parcours en profondeur.

3.5. Parcours en profondeur d'un graphe non connexe

Lors d'un parcours en profondeur d'un graphe non connexe d'ensemble de sommets $V = \db{0,n-1}$, on commence par effectuer un parcours en profondeur à partir du sommet $0$, puis on recommence, à partir du premier sommet non encore visité, etc.

Décrire l'ordre du parcours en profondeur pour le graphe ci-contre.
Écrire une fonction choisir_nouveau_sommet qui prend en argument un graphe et une liste de sommets à éviter, et qui renvoie le premier sommet du graphe qui n'appartient pas à la liste donnée.
Écrire une fonction parcours_profondeur qui prend en argument un graphe et qui affiche la liste des sommets, dans l'ordre dans lequel ils sont visités par un parcours en profondeur.
Proposer une modification de l'algorithme, pour éviter une complexité en $O(n^2)$ quand le graphe n'a presque pas d'arc (un graphe vide par exemple).

Avec cette amélioration, la complexité est en $O(n+m)$.

3.6. Cycles

Un cycle dans un graphe orienté est un chemin fermé non vide, c'est-à-dire un chemin non trivial d'un sommet à lui-même.
Un cycle dans un graphe non orienté est un chemin fermé non vide, qui ne revient pas directement sur ses pas, c'est-à-dire qui ne passe pas deux fois de suite par la même arête.

Écrire une fonction a_cycle_naif qui prend en argument un graphe orienté et décide si ce graphe admet un cycle ou non. ¹
★ Écrire une fonction a_cycle_sym qui prend en argument un graphe non orienté et connexe, et qui renvoie True si le graphe a un cycle. ²

On veut une complexité en $O(n+m)$.
★ Écrire une fonction a_cycle, fonctionnant pour un graphe orienté, d'une complexité en $O(n+m)$. ³

Chemins et cycles élémentaires

Un chemin est dit élémentaire s'il ne passe pas deux fois par un même sommet.
Un cycle est dit élémentaire si, mis à part ses deux sommets extrémaux, il ne passe pas deux fois par le même sommet.

De tout chemin $s \ra s'$, on peut extraire un chemin élémentaire de mêmes sommets extrémaux.

On représente un cycle par une liste des sommets consécutifs, le premier et le dernier coïncidant.

Écrire une fonction cycles_élém qui prend en argument un cycle et renvoie la liste des cycles élémentaires qui le composent.
Quelle est la complexité ? Peut-on faire mieux ?

Soit $\delta\geq 2$ et $G$ un graphe non orienté dont tous les sommets sont de degré $\geq \delta$. Montrer que $G$ admet un cycle élémentaire de longueur $\geq \delta + 1$.

Indication : Considérer un chemin de sommets distincts de longueur maximale.

Arbres et forêts

Un graphe connexe non orienté sans cycles est appelé un arbre.

Tout graphe connexe non orienté sans cycles est réunion de ses composantes connexes, chacune étant un arbre.

On considère des graphes non orientés.

Montrer que tout graphe avec $n$ sommets et au moins $n$ arêtes admet un cycle.
Montrer qu'un arbre sur $n$ sommets admet exactement $n-1$ arêtes.
Montrer qu'un graphe de $n$ sommets, tous de degré $\geq k$ admet un cycle élémentaire de longueur au moins $k+1$.

★ Autres

Π Montrer qu'un graphe non orienté est biparti si et seulement si tous ses cycles ont une longueur paire.
Écrire une fonction pibartition qui prend en argument un graphe biparti et renvoie une bipartition.

Étant donné $\mc G$ orienté acyclique, un tri topologique de $\mc G$ est une association injective, à chaque sommet $s$, d'une valeur $h(s)\in\db{1,n}$ telle que $\forall i,j\in S,\, i\ra j \Rightarrow h(i)\leq h(j)$.

Écrire une fonction tri_top qui renvoie une telle association. Pour simplifier, on pourra supposer qu'un parcours en profondeur issu du premier sommet parcourt tout le graphe.

Indication : Il est (presque) obligatoire d'écrire une version récursive.

3.7. Modélisation

Une grille $n\times m$ de nombres $0$ ou $1$ est représentée par une liste de liste G. La valeur $1$ signifie que la case est obstruée. Écrire une fonction qui prend en argument en argument deux positions $(i_1,j_1)$ et $(i_2, j_2)$ et qui décide si on peut se déplacer de la case $(i_1,j_1)$ à $(i_2, j_2)$ par pas d'une unité dans les quatre directions canoniques en restant sur des cases non obstruées.

On place une dame en position d5 sur un échiquier, et un cavalier en position h8. La dame ne bouge pas, et le cavalier peut se déplacer selon les règles des échecs. Est-il possible pour le cavalier de visiter toutes les cases possibles de l'échiquier, sans jamais être menacé par la dame, ni la prendre ? Si oui, afficher un tel parcours.

Cavalier Dame.png

Écrire des fonctions cherchant des solutions aux deux problèmes suivants.

Lulu doit faire passer le chou, la chèvre et le loup de l'autre côté de la rivière. Mais il n'a qu'une place sur son bateau !

De plus, si la chèvre et le chou sont ensemble sur une rive quand Lulu s'éloigne, la chèvre mange le chou. Et si le loup et la chèvre sont ensemble quand Lulu s'éloigne, le loup mange la chèvre !

Est-il possible de faire traverser tout le monde ?
Lulu doit faire passer le chou, la chèvre, le loup, le bâton et le feu de l'autre côté de la rivière. Mais il n'a que deux places sur son bateau !

De plus,
- si la chèvre et le chou sont ensemble sur une rive quand Lulu s'éloigne, la chèvre mange le chou,
- si le loup et la chèvre sont ensemble quand Lulu s'éloigne, le loup mange la chèvre,
- si le bâton et le loup sont ensemble quand Lulu s'éloigne, le bâton bat le loup,
- si le feu et le bâton sont ensemble quand Lulu s'éloigne, le feu brûle le bâton.
Est-il possible de faire traverser tout le monde ?

4. Compléments

4.1. Parcours eulérien et hamiltonien

Dans un graphe $G$ non orienté

Un chemin eulérien est un chemin qui passe par toutes les arêtes exactement une fois.
Un chemin hamiltonien est un chemin qui passe par tous les sommets exactement une fois.
Un cycle eulérien ou hamiltonien est un tel chemin qui revient à son point de départ.

La recherche d'un chemin ou d'un cycle eulérien n'est pas très compliquée. Par contre, la recherche d'un chemin ou d'un cycle hamiltonien est un problème NP-complet, qui n'admet pas de solution avec une complexité polynomiale.

Soit $G$ un graphe connexe non orienté. Alors $G$ admet un circuit eulérien (un cycle qui passe par chaque arête exactement une fois) si et seulement si tous ses sommets sont de degrés pairs.

Démontrer le théorème d'Euler.

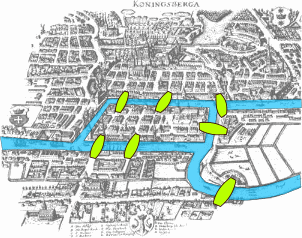
La ville russe de Königsberg (aujourd'hui Kaliningrad) est découpée par le fleuve Pregolia. Les rives sont reliées par 7 ponts historiques. Le problème consiste à déterminer s'il existe ou non une promenade dans les rues de Königsberg permettant, à partir d'un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ.

Ce problème est équivalent à la recherche d'un cycle eulérien dans un multi-graphe, dont les arêtes sont les ponts (elles sont multiples : deux sommets peuvent être reliés par plusieurs arêtes). Le théorème d'Euler s'applique encore dans ce contexte, et implique qu'un tel cycle n'existe pas.

Une suite de de Bruijn d'ordre $n$ sur un alphabet $\mc A$ est un mot cyclique sur l'alphabet $\mc A$ qui contient tous les facteurs de taille $n$ une et une seule fois.

Par exemple, pour $\mc A = \{0,1\}$ et $n = 3$, le mot cyclique $\om = 00010111$ contient les $8$ facteurs de taille $3$ possibles.

Justifier qu'un mot de de Bruijn est de longueur $|\mc A|^n$.
Décrire un graphe orienté $G_1$ tel que la recherche d'un mot de de Bruijn soit équivalente à la recherche d'un cycle hamiltonien dans $G_1$.
Décrire un graphe orienté $G_2$ tel que la recherche d'un mot de de Bruijn soit équivalent à la recherche d'un cycle eulérien dans $G_2$

Montrer que toute orientation du graphe complet $K_n$ admet un chemin hamiltonien.

Indication : Procéder par récurrence.

Soit $G$ un graphe non orienté à $n$ sommets de degrés $\geq \frac{n}{2}$.

Montrer que $G$ est connexe.
★ Montrer que $G$ admet un cycle hamiltonien, c'est-à-dire un cycle qui passe exactement une fois par chaque sommet.

Indication : Considérer un plus long chemin de sommets distincts, de longueur $t$. Commencer par montrer qu'on peut trouver un cycle de longueur $t$.

4.2. Graphes planaires

Un graphe est dit planaire s'il peut être représenté dans le plan, sans qu'aucune de ses arêtes n'en croise une autre.

Une représentation dans le plan définit des faces, qui sont les composantes connexes du plan $\R^2$ auquel on retire les courbes des arêtes du graphe. En particulier, il existe une (unique) face infinie.

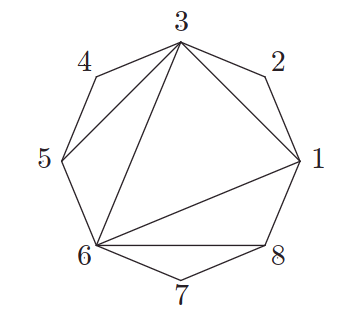
Ci-contre, un graphe à $n = 8$ sommets, $a = 10$ arêtes, et $f = 7$ faces.

Si l'on dessine un graphe planaire connexe dans le plan, en notant $n$ le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces, on a $$n-a+f=2$$

Par récurrence sur le nombre de faces. Si $f = 1$, alors le graphe n'admet aucun cycle. Étant connexe, c'est un arbre, avec $n$ sommets et $n-1$ arêtes.

On considère un graphe à $f\geq 2$ faces. Comme ce n'est pas un arbre, il admet un cycle. En retirant une arête du cycle, on fusionne deux faces, et l'on préserve la connexité du graphe. Si la formule d'Euler est correcte pour le graphe obtenu, elle l'est également pour le graphe d'origine.

Dans le plan, on considère trois maisons $A,B,C$, qui doivent chacune être reliée par des tuyaux à trois usines $W,G,E$ pour être alimentée en eau, en gaz, et en électricité.

En utilisant la formule d'Euler, justifier qu'il n'est pas possible de faire ces liaisons sans qu'elles se croisent.

Autrement dit, le graphe biparti complet $K_{3,3}$ n'est pas planaire.

Graphe dual

Le graphe dual $G'$ d'un plongement $G$ d'un graphe planaire est le graphe dont les sommets sont les faces de $G$, qui sont reliées si elles sont contiguës dans $G$.

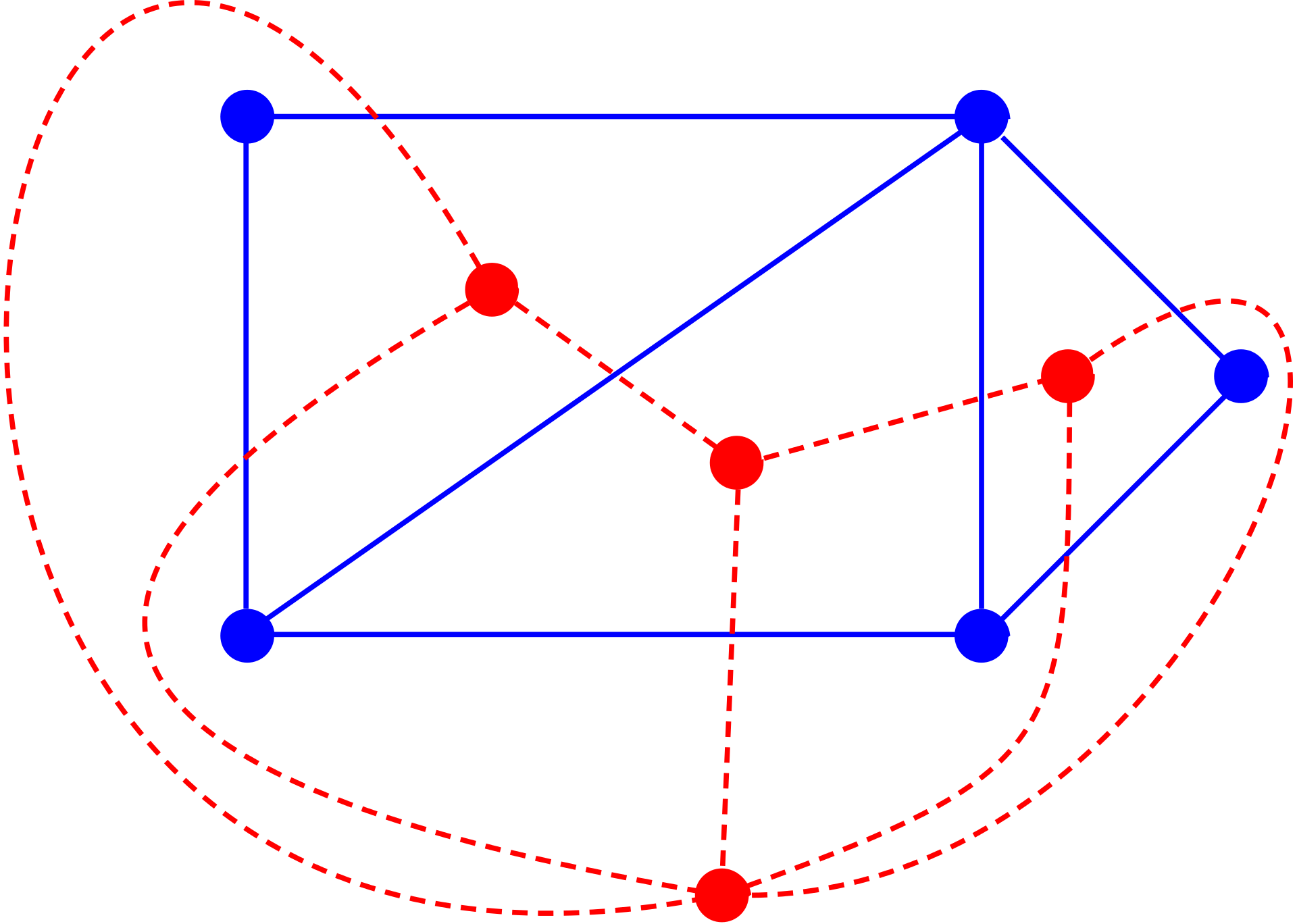
Ci-contre, en trait plein un graphe $G$, et en pointillé son graphe dual.

En fait le graphe dual est un multi-graphe : il peut y avoir plusieurs arcs d'un sommet $s$ à un sommet $s'$, comme dans l'exemple ci-contre.

Graphe dual.png

Les deux rives d'une rivière sont reliées par un système de $13$ ponts comme sur la figure. Lors d'une innondation, chaque pont a une probabilité $\frac{1}{2}$ d'être détruit, indépendamment des autres. Quelle est la probabilité de pouvoir toujours passer d'une rive à l'autre après une inondation ?

Indication : Considérer le graphe dual, ou la probabilité qu'un bateau à mât puisse traverser le système de ponts de haut en bas après une inondation.

$$\left|\begin{array}{ccccc} \ldots & O & \ldots & O & \ldots \\ & \vdots & & \vdots & \\ \ldots & O & \ldots & O & \ldots \\ & \vdots & & \vdots & \\ \ldots & O & \ldots & O & \ldots \end{array}\right|$$

Triangulation

On considère un $n$-polygone régulier $\mc P$. Une triangulation de $\mc P$ est un ensemble de cordes reliant des sommets non contigus de $\mc P$ de sorte qu'aucune paire de cordes ne se coupe et que toutes les faces à l'intérieur de $\mc P$ définies par les $n$ cotés de $\mc P$ et les cordes soient des triangles.

Soit $\mc T$ une triangulation, avec $c$ cordes et $f$ faces.

Montrer que $n + 2c = 3f$.
Montrer que $f = c + 1$.
En déduire une expression de $c$ en fonction de $n$.

Notes de bas de page:

Un graphe orienté a un cycle si et seulement s'il existe un sommet $s$ tel qu'un parcours en profondeur du graphe à partir de $s$ retombe sur $s$ au bout d'un moment.

$G$ a un cycle si et seulement si le parcours en profondeur (ou largeur) partant de $s$ voit plusieurs fois un même sommet, sans compter la possibilité de revenir directement sur ses pas.

Le graphe admet un cycle si et seulement si un des sommets admet comme successeur un de ses ancêtres dans le parcours en profondeur (d'un graphe non nécessairement connexe)